Could a human enter a black hole to study it?

Could a human enter a black hole to study it?  

Pulkeet, age 12, Bahadurgarh, Haryana, India

To solve the mysteries of black holes, a human should just venture into one. However, there is a rather complicated catch: A human can do this only if the respective black hole is supermassive and isolated, and if the person entering the black hole does not expect to report the findings to anyone in the entire universe.

We are both physicists who study black holes, albeit from a very safe distance. Black holes are among the most abundant astrophysical objects in our universe. These intriguing objects appear to be an essential ingredient in the evolution of the universe, from the Big Bang till present day. They probably had an impact on the formation of human life in our own galaxy.

Two types of black holes

The universe is littered with a vast zoo of different types of black holes.

They can vary by size and be electrically charged, the same way electrons or protons are in atoms. Some black holes actually spin. There are two types of black holes that are relevant to our discussion. The first does not rotate, is electrically neutral – that is, not positively or negatively charged – and has the mass of our Sun. The second type is a supermassive black hole, with a mass of millions to even billions times greater than that of our Sun.

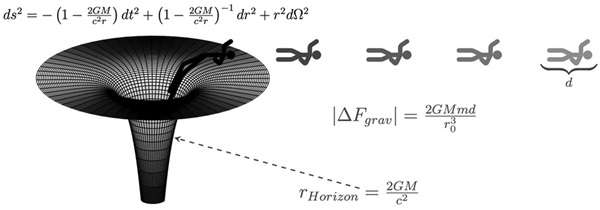
Besides the mass difference between these two types of black holes, what also differentiates them is the distance from their center to their “event horizon” – a measure called radial distance. The event horizon of a black hole is the point of no return. Anything that passes this point will be swallowed by the black hole and forever vanish from our known universe.

At the event horizon, the black hole’s gravity is so powerful that no amount of mechanical force can overcome or counteract it. Even light, the fastest-moving thing in our universe, cannot escape – hence the term “black hole.”

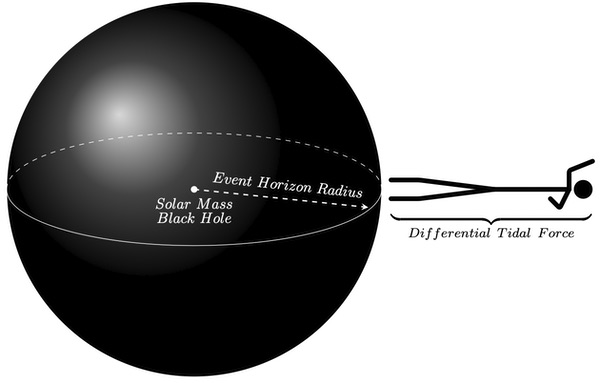
The radial size of the event horizon depends on the mass of the respective black hole and is key for a person to survive falling into one. For a black hole with a mass of our Sun (one solar mass), the event horizon will have a radius of just under 2 miles.

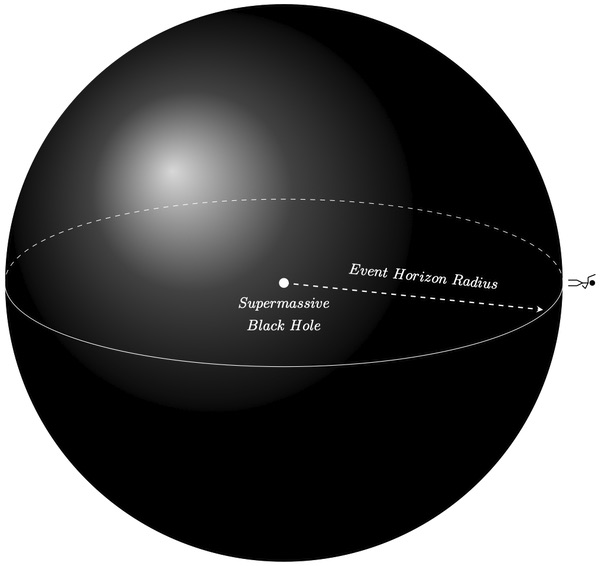
The supermassive black hole at the center of our Milky Way galaxy, by contrast, has a mass of roughly 4 million solar masses, and it has an event horizon with a radius of 7.3 million miles or 17 solar radii.

Thus, someone falling into a stellar-size black hole will get much, much closer to the black hole’s center before passing the event horizon, as opposed to falling into a supermassive black hole.

This implies, due to the closeness of the black hole’s center, that the black hole’s pull on a person will differ by a factor of 1,000 billion times between head and toe, depending on which is leading the free fall. In other words, if the person is falling feet first, as they approach the event horizon of a stellar mass black hole, the gravitational pull on their feet will be exponentially larger compared to the black hole’s tug on their head.

The person would experience spaghettification, and most likely not survive being stretched into a long, thin noodlelike shape.

Now, a person falling into a supermassive black hole would reach the event horizon much farther from the the central source of gravitational pull, which means that the difference in gravitational pull between head and toe is nearly zero. Thus, the person would pass through the event horizon unaffected, not be stretched into a long, thin noodle, survive and float painlessly past the black hole’s horizon.

Other considerations

Most black holes that we observe in the universe are surrounded by very hot disks of material, mostly comprising gas and dust or other objects like stars and planets that got too close to the horizon and fell into the black hole. These disks are called accretion disks and are very hot and turbulent. They are most certainly not hospitable and would make traveling into the black hole extremely dangerous.

To enter one safely, you would need to find a supermassive black hole that is completely isolated and not feeding on surrounding material, gas and or even stars.

Now, if a person found an isolated supermassive black hole suitable for scientific study and decided to venture in, everything observed or measured of the black hole interior would be confined within the black hole’s event horizon.

Keeping in mind that nothing can escape the gravitational pull beyond the event horizon, the in-falling person would not be able to send any information about their findings back out beyond this horizon. Their journey and findings would be lost to the rest of the entire universe for all time. But they would enjoy the adventure, for as long as they survived … maybe ….