The problem is that during the night the Moon sails across the vast vault of the sky unrivaled in size. During the day, only the Sun (which we should never look at without proper protection) compares to the Moon in apparent size. Furthermore, when the Moon lies just above the horizon, a physiological effect called the Moon illusion causes its image to swell in the mind’s eye. And when the Moon stands high overhead, another illusion makes it appear smaller than it should.
Few would argue that a Full Moon rising attracts attention. But I’ve noticed a greater “Wow!” factor when people see a perigee Full Moon rising. Arguably, then, we can detect the difference, at least on a subconscious level. But can we perform a more reliable test?
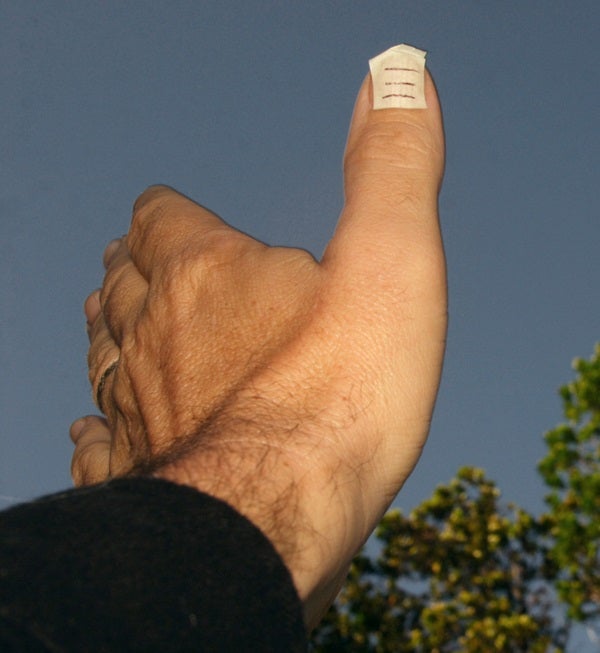
Over the years, I’ve enjoyed experimenting with the challenge noted above and have found a simple solution. Just go outside when the Moon is visible in the daytime sky, hold out your thumb at arm’s length, and point it toward the Moon. With both eyes open, first focus on your thumb, then on the Moon. What happens?
When you shift focus, your thumb should look doubled (the effect of parallax). Depending on your dominant eye, one of the thumbs will appear transparent enough for you to project the Moon against the phantom thumbnail! If you do this when the Moon is at apogee, then at perigee, you can detect a noticeable difference in the size of the Moon compared to the size of your nail.
Independently, Texas A&M University astronomer Kevin Krisciunas has also given this matter some thought. While teaching his students, Krisciunas began to wonder about the ancient Greeks and naked-eye Renaissance observers who long knew that the Earth-Moon distance varies — knowledge deduced primarily from observations of the Moon’s size during total and annular solar eclipses.
But those observed changes in size could have been due to the variable Earth-Sun distance or Earth-Moon distance, or both. “So,” Krisciunas pondered, “can we measure (without any lenses) the Moon’s correct angular size, and that the Earth-Moon distance varies by plus or minus 5 percent?”
To find out, Krisciunas designed an experiment. Using a hole punch, he took a thin piece of cardboard and made a hole 0.24 inch (6.2 millimeters) across. He then attached the cardboard to a cross piece that could slide along a yardstick. By simply pointing the yardstick at the Moon and moving the cardboard back and forth, Krisciunas could match the Moon’s angular size with the hole’s angular size.
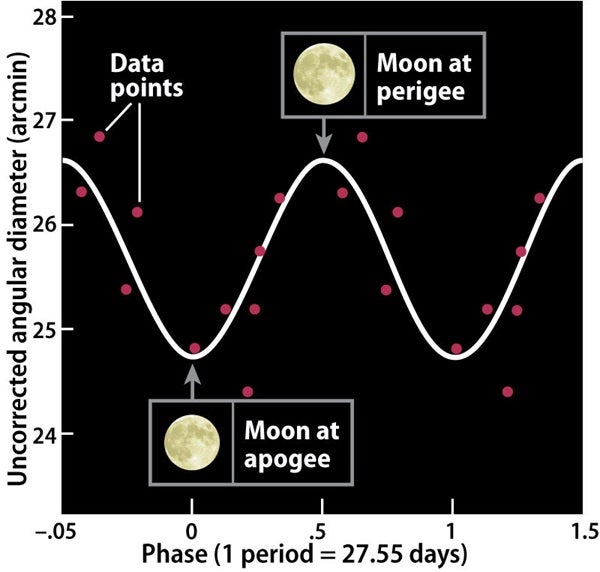
A hole 0.24 inch across, held 27.05 inches (687mm) from the eye, should subtend an angle of 31 arcminutes — the Moon’s average angular diameter. But that’s not what he found. Using the following equation: θ = 60 × (h/d) × (180/π) where θ is the Moon’s angular extent in arcminutes, h is the diameter of the hole (0.24 inch), and d is the distance of the hole from the eye (which he determined to be 32.56 inches [827mm]), Krisciunas determined θ to be only approximately 26 arcminutes.
As Krisciunas discovered, and as the late Marcel Minnaert suggested in his 1954 book The Nature of Light and Color in the Open Air, psychological factors that are little understood play a role in perceiving the Moon. Indeed, Minnaert stated that if you look at the Moon through an aperture in a piece of cardboard with one eye, the Moon will appear smaller than when viewed directly with two eyes.
Undaunted, Krisciunas took a disk 0.358 inch (9mm) in diameter and taped it to a door 32.8 feet (10 meters) away, so that its angular size would equal 31 arcminutes. When he looked at that disk through the 0.24-inch hole at a distance of 32.3 inches (821mm), he found a match of angular size (26 arcminutes). If we therefore divide the Moon’s true average angular extent (31 arcminutes) by the measured average (26 arcminutes), we arrive at a correction factor of 1.2.
“If I take my uncorrected measures of the angular diameter of the actual Moon and multiply them by 1.2,” Krisciunas says, “I get, on average, the correct angular size of the Moon accurate to plus or minus 0.8 arcminute. I’ve convinced myself [that] with my very simple equipment I can measure the variation of the Moon’s angular size and eliminate systematic errors with my correction factor” (see graph above).
Krisciunas cautions, however, that everyone’s eyes are different; observers may have to find their own correction factors. He’d like to know if you get the same correction factors for objects that are demonstrably 31 arcminutes wide, using a sighting hole that is about 0.24 inch.
If a 0.35-inch circle viewed at a distance of 32.8 feet comes out to 31 arcminutes, then your correction factor is 1. If you derive an angular size less than 31 arcminutes, then your correction factor is greater than 1, like Krisciunas’.
After speaking with Krisciunas, I took a piece of ½-inch masking tape on which I had penned a couple of measurement lines, and placed it on my thumbnail. I went outside, casually held my thumb up to the Moon, and measured the Moon’s north-south extent against the ruled lines. Next I measured the distance from my dominant eye to my extended thumb. Back inside, I measured the Moon’s projected size on the tape with a ruler.
The result? At that date and time, the Moon was 32 arcminutes in apparent diameter. My measurement? 34 arcminutes, off by only 6 percent … not bad for a casual experiment! I know I can do better, and I bet you can, too!
Krisciunas and I would love to hear about your experiences. Send reports to krisciunas@physics.tamuedu and someara@interpac.net.
February 2010: Readers search for shadow bands
See an archive of Stephen James O’Meara’s Secret Sky