For one, no scientist can explain precisely what happened during the first second. Einstein’s general theory of relativity breaks down at the extraordinary temperatures and densities just after the Big Bang. For another, theorists have added several major components to the model. Dark matter, dark energy, and inflation all were added to the standard model to help it match ever-more-accurate observations.
These uncertainties helped motivate cosmologists Paul J. Steinhardt of Princeton University and Neil Turok of Cambridge University to develop a theory they call the “cyclic model of the universe.” The model envisions a universe that undergoes limitless cycles. Each cycle begins with a Big Bang, is followed by a long period of expansion and cooling, and ends with a Big Crunch. The cycle repeats perhaps once every trillion years. The Big Bang that launched our current universe is just the latest in a long line of such bangs.
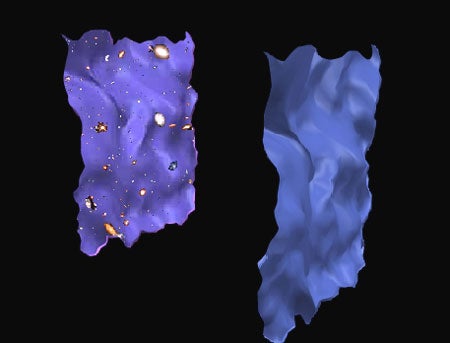
This animation shows a simplified view of the cyclic model. Our universe exists on a three-dimensional membrane, or “brane” for short, near a second such brane. (The distance between the branes lies along a fourth spatial dimension.) In the animation, the two-dimensional sheet on the left represents our brane.
The animation begins with the two branes at their maximum separation. Gravitational and springlike forces then draw the branes together, and quantum fluctuations form wrinkles in the branes. The branes then collide — the Big Bang. Matter and radiation develop as the branes bounce apart. As our brane expands and cools, galaxies form. But after some 9 billion years, dark energy starts to take over. The branes expand ever-more rapidly, diluting the universe’s matter and radiation. Dark energy ultimately smoothes and flattens the universe, restoring it to a pristine condition ready to begin another cycle.
You can learn more about the cyclic model at the web site of the book Endless Universe: Beyond the Big Bang by Paul J. Steinhardt and Neil Turok. For a more in-depth look at the model (and Steinhardt’s other research interests), visit Paul Steinhardt’s homepage.